Journey through New York Journeys
My brother once pointed out something to me about New York City: any two points in the city are either 20 minutes or 45 minutes apart. This may seem impossible, but if you ask any New Yorker they’ll confirm.
This got me thinking though - can we create a space where the distance between any two points is either 20 or 45?
Barring NYC - which of course refuses to bend to the laws of time and space - what we’re looking for is a graph. Specifically, a weighted, undirected graph that meets the following criteria:
- There must be a path of edges to get from any vertex to any other (the graph must be connected).
- The fastest route (path with minimum weight) must be either 20 or 45.
- Any edge connecting two vertices must be the minimum path.
If a graph meets this criteria, we'll call it New York Valid (NYV).
To illustrate that third rule, consider the graphs below. In the second one, the AB edge would never be used, because the A-C-B route is faster. We'll denote that an illegal 3-cycle.
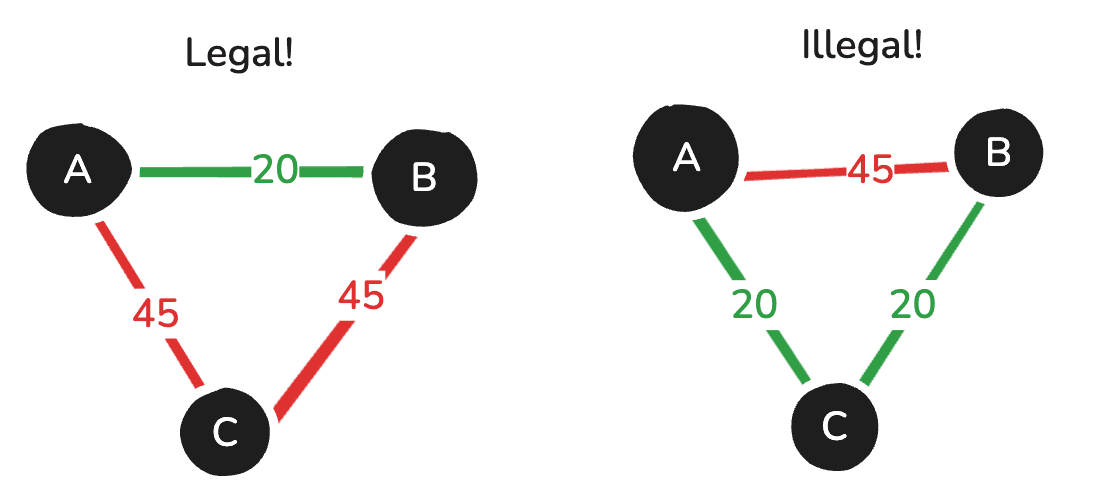
Note: that rule is essentially the triangle inequality theorem - not as it applies to actual triangles in Euclidean space (since we don’t require edges to be straight or anything) but the measure theory version, which refers to generalized distances in a metric space. Also, we'll use the term distance from now on to mean the minimum distance (or measure of the minimum weighted path).
So first off, what's the most vertices we can have in an NYV graph?
This is actually trivial - we can create the complete graph (an edge between every pair of vertices) for any size n, and any configuration of edge weights 20 and 45 that avoid an illegal 3-cycle.

It would be annoying to have to check that every contained triangle is legal, especially when N gets big. I think I've found a better way, though.
Proposition: An NYV is legal if and only if the components of the subgraph induced by the edges of length 20 are each fully connected.
I won’t formally prove this, but I’ll explain my reasoning, which hopefully is sound.
A 3-cycle contains 3 points. An illegal 3-cycle must be 45-20-20. Suppose a-b is 20 and b-c is 20. All 3 points must be in the same component of the induced subgraph. Since the subgraph is fully connected, a-c must be 20, which means the cycle is legal. Justifying the other direction (all cycles legal implies full connectedness) works similarly.
Maybe we can make things a bit more interesting by looking for planar NYVs - that is, we can embed it in 2D space without any of the edges crossing.
Unfortunately this turns out not to be very exciting either. Here’s the problem: if our graph isn’t fully connected, there must be two vertices that are connected by a path of length 2 (length being the actual number of edges.) Since 20 + 20 is not 45 - according to Wolfram Alpha at least – the weight of that path won’t be 20 or 45, which means our graph isn’t NYV. Longer paths fail for the same reason. So our maximum NYV will be the largest fully-connected graph that can be embedded in 2D space, .

Thankfully, we can make things a little more interesting.
Expanding our edge options
Okay, let’s add an additional option to our travel set: if the minimum path weight between any two nodes is 45, 20, or 25, we'll call the graph Expanded New York Valid (ENYV).
What's the most nodes we can have in a planar ENYV?

Now we're getting somewhere!
The largest planar ENYV I've been able to find has order 9. And she's a beauty.

What's next?
So here’s a few questions to chew over. I don’t know the answer to either, but they could be worth exploring:
Given a set of distance options and an integer
- How many distinct ENYV’s are there?
- Does there exist a planar ENYV for ?
I'll probably dive deeper into this soon. It will probably involve some algebraic topology, or - if we're really unlucky - additive combinatorics.
If you have ideas about either question, let me know. And hit me up if you’re in NYC - I can be there in either 20 or 45 minutes.